Matematisk løsning med lpSolve i R

I dette indlæg viser jeg, hvordan man udfører simpel lineær optimering i R. Du kan også finde andre indlæg skrevet af mig, der ser på andre lineære optimeringsopgaver, såsom transportproblemet (kan løses med lp.transport), opgaveproblemet ( kan løses med lp.assign) og heltals lineær programmering (også lineære blandede heltalsproblemer kan løses i R).

Lineær programmering anvendes i vid udstrækning til modellering af faciliteters placeringsproblemer. lpSolve er en udvidelse tilgængelig i R, der giver adgang til en C-baseret grænseflade til løsning af lineære programmeringsproblemer. Da grænsefladen er udviklet i C, har den maksimal ydeevne, hvilket minimerer den tid, der kræves til at løse lineære programmeringsproblemer uden at skulle skifte programmeringsmiljø eller programmeringssprog.

I dette indlæg giver jeg et eksempel på et simpelt lineært programmeringsproblem løst med lpSolve.

Den objektive funktion er at maksimere omsætningen defineret af funktionen f(x,y) = 2x + 3y, med forbehold for begrænsningerne, at x, y er ikke-negative og x + y ikke større end 3.

Som internettet vil vise dig, er dette problem let at løse, dvs. ved at tegne et linjeplot eller ved at anvende simplex-algoritmen. Jeg vil ikke forklare algoritmerne eller metodikken til løsning af lineære problemer i detaljer, men jeg vil give et kort eksempel på, hvordan dette simple problem kan modelleres og løses ved hjælp af lpSolve i R. Bagefter vil jeg vise en grafisk illustration, som verificerer resultatet.

Jeg indlæser lpSolve-pakken (har allerede installeret den) og modellerer problemet ved hjælp af lpSolve API:

library(lpSolve)
f.obj <- c(2,3)                           # coefficient vector of objective function
f.con <- matrix(c(1,1),nrow=1,byrow=TRUE) # coefficient matrix for constraint matrix
f.dir <- c("<=")                          # constraint direction vector
f.rhs <- c(3)                             # constraint values

Lad os nu løse det lineære problem:

solution <- lp("max",f.obj,f.con,f.dir,f.rhs)
solution

## Success: the objective function is 9

Den optimale løsning er følgende (optimal x- og y-værdi for det aktuelle problem):

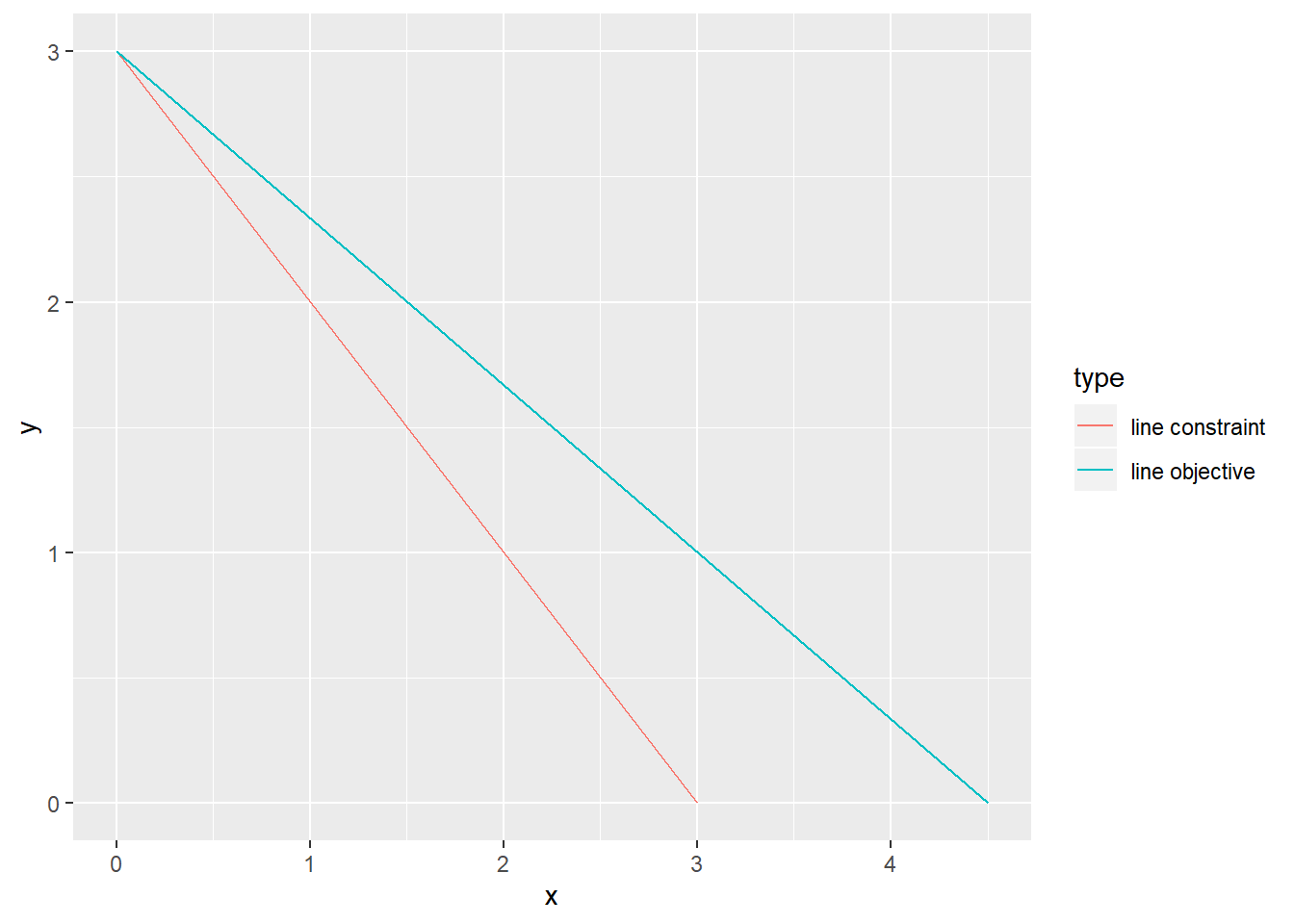
solution$solution

## [1] 0 3

Lad os nu grafisk verificere resultatet. Jeg definerer to linjer, som jeg visualiserer ved hjælp af geom_line fra ggplot2-pakken. Den første linje repræsenterer begrænsningen om, at x + y ikke må være større end 3, den anden linje repræsenterer objektivfunktionen. Linjen for målfunktionen repræsenterer dens maksimalt opnåelige værdi, dvs. den optimale værdi. Linjen for begrænsningen repræsenterer dens bindingstilfælde, dvs. når den er nøjagtigt lig med 3. I mere enkle vendinger: “line objektiv” : 2x + 3y = 9 “line constraint” : x + y = 3

library(ggplot2)
plot_df <- as.data.frame(matrix(nrow=4,ncol=3))
colnames(plot_df) <- c("x","y","type")
plot_df$x <- c(0,3,0,9/2)
plot_df$y <- c(3,0,9/3,0)
plot_df$type <- c("line constraint","line constraint", "line objective", "line objective")
ggplot(plot_df) + geom_path(mapping = aes(x=x,y=y,color=type))

I betragtning af at x+y=3, kan du så se, at den optimale løsning på dette problem må være x=0, y=3 – og at dette maksimerer den objektive funktion?

Hvis du er interesseret i ikke-lineær programmering (f.eks. gradient descent med nloptr) eller kvadratisk optimering (quadprog) i R, så gå videre og tjek også mine andre indlæg om disse typer optimeringsopgaver.