Lineær optimering i Python med SciPy

I dette indlæg viser jeg hvordan du kan løse lineære problemer i Python. Jeg vil løse følgende problem:

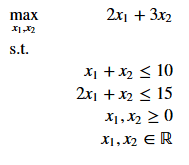
SciPy-modulet i Python indeholder linprog-funktionen. Med linprog kan du beskrive og løse lineære problemer. Dertil skal de beskrives som minimeringsproblemer i vektor-matrix-form. Forneden kan du se en generisk beskrivelse:

Problemet kan nu løses i Python:

# definer en vektor for funktionen som skal optimeres
c = [-2,-3]

# definer en matrix med koefficienterne af alle begrænsede funktioner (betingelser)
A_ub = [[1,1],
        [2,1]]

# en liste med alle begrænsende værdier (grænser)
b_ub =[10,15]

# en tuple for hver optimeringsvariabel, med min og max værdi
x1_bounds = (0,None)
x2_bounds = (0,None)

# nu kan jeg importere linprog fra SciPy.optimize
from scipy.optimize import linprog
model_linear = linprog(c=c,
                      A_ub=A_ub,
                      b_ub = b_ub,
                      bounds = [x1_bounds,x2_bounds])

# model_linear indeholder løsningen; derfor udskriver jeg objektet
print(str(model_linear))

     fun: -30.0
 message: 'Optimization terminated successfully.'
     nit: 1
   slack: array([ 0.,  5.])
  status: 0
 success: True
       x: array([  0.,  10.])

Idet vi transformerede vores problem fra max- til min-form vendte jeg fortegnet på koefficienterne i den objektive funktion om, fra plus til minus. Når vi interpreterer resultat skal vi huske at vende fortegnene om igen, fra minus til plus.

Den optimale løsning er x1=0,x2=10 og den optimale værdi er 30. Den første betingelse er bindende (“slack” = 0), mens den anden betingelse har en “slack” på 5. Den anden betingelse er løs og ikke bindende.