내 게시물 중 일부에서 선형 최적화 문제를 해결하기 위해 R에서 lpSolve 또는 FuzzyLP를 사용했습니다. 또한 이러한 문제를 해결하기 위해 Python에서 PuLP 및 SciPy.optimize를 사용했습니다. 이 모든 경우에 문제는 하나의 목적 함수만을 가졌습니다.
이 게시물에서는 다중 목표 선형 최적화 문제를 해결하기 위해 PuLP 모듈을 사용하여 Python으로 코딩 예제를 제공하고 싶습니다.
다목적 선형 최적화 문제는 하나 이상의 목적 함수가있는 선형 최적화 문제입니다. 이 선형 프로그래밍 영역은 다중 목표 선형 프로그래밍 또는 다중 목표 선형 프로그래밍이라고도합니다.
아래에서는 두 가지 목적 함수가있는 예문 다목적 선형 최적화 문제를 설명했습니다.

위의 문제 설명에서 두 가지 목적 함수가 예를 들어 두 가지 다른 목표를 나타낸다고 가정합니다. 일부 제품 포트폴리오의 서비스 수준과 수익 마진에 대해이 문제를 해결하기위한 두 가지 대안을 테스트합니다.
첫 번째 접근 방식은 목표 중 하나를 해결 한 다음 두 번째 최적화 실행에 추가 제약 조건을 추가하여 첫 번째 문제의 최적 결과에서 문제를 수정 한 다음 두 번째 목적 함수를 최대화하는 것입니다 ( 첫 번째 하위 문제에 대한 최적의 목표 값 유지).
두 번째 접근 방식은 두 목표를 함께 추가하는 것입니다. 즉 가중치를 적용하여 하나의 목적 함수로 병합하는 것입니다. 가중치를 샘플링하고 각 샘플링 된 가중치에 대해 결합 된 문제를 풀면 가중치에 따라 최적의 결과를 검토 할 수 있습니다.
접근법 1 : 하나의 목표를 최대화 한 다음이를 제약 조건으로 추가하고 다른 목표를 해결합니다.
PuLP를 사용하여 첫 번째 목표를 먼저 최대화 한 다음 해당 목적 함수를 원래 문제에 대한 제약으로 추가하고 추가 제약을 포함하여 모든 제약에 따라 두 번째 목적을 최대화합니다.
수학적 구문에서 우리가 먼저 해결하는 문제는 다음과 같이 나타낼 수 있습니다.

다음은 PuLP 모듈을 사용하여 Python에서 위의 문제 설명을 구현 한 것입니다.
# 먼저 PuLP 가져 오기
import pulp
# 그런 다음 문제의 초기 선언을 수행합니다.
linearProblem = pulp.LpProblem("Maximizing for first objective",pulp.LpMaximize)
# PuLP를 사용하여 최적화 변수 선언
x1 = pulp.LpVariable("x1",lowBound = 0)
x2 = pulp.LpVariable("x2",lowBound = 0)
# 선형 문제 설명에 (첫 번째) 목적 함수 추가
linearProblem += 2*x1 + 3*x2
# 문제에 제약을 추가
linearProblem += x1 + x2 <= 10
linearProblem += 2*x1 + x2 <= 15
# 기본 솔버로 해결하여 첫 번째 목표를 최대화합니다.
solution = linearProblem.solve()
# 최적이 발견되면 출력 정보, 최대 목표 값 및 최적 지점이 무엇인지
print(str(pulp.LpStatus[solution])+" ; max value = "+str(pulp.value(linearProblem.objective))+
" ; x1_opt = "+str(pulp.value(x1))+
" ; x2_opt = "+str(pulp.value(x2)))
Optimal ; max value = 30.0 ; x1_opt = 0.0 ; x2_opt = 10.0
이제 추가 제약 조건에 따라 두 번째 목적 함수가 최대화되도록 원래 문제를 다시 설명합니다. 이 추가 제약은 첫 번째 목표가 30 개 이상이어야한다고 요구합니다. 수학적 구문을 사용하여 지금 해결하는 문제를 다음과 같이 나타낼 수 있습니다.

다음은 PuLP를 사용하여 Python에서 위의 문제 설명을 구현 한 것입니다.
# 문제 진술 리모델링
linearProblem = pulp.LpProblem("Maximize second objective",pulp.LpMaximize)
linearProblem += 4*x1 - 2*x2
linearProblem += x1 + x2 <= 10
linearProblem += 2*x1 + x2 <= 15
linearProblem += 2*x1 + 3*x2 >= 30
# 리모델링 후 문제 진술 검토
linearProblem
Maximize_second_objective:
MAXIMIZE
4*x1 + -2*x2 + 0
SUBJECT TO
_C1: x1 + x2 <= 10
_C2: 2 x1 + x2 <= 15
_C3: 2 x1 + 3 x2 >= 30
VARIABLES
x1 Continuous
x2 Continuous
이제 PuLP의 기본 솔버를 사용하여이 문제를 해결합니다.
# 기본 솔버 적용
solution = linearProblem.solve()
# 최적이 발견되었는지 여부를 요약 한 문자열을 출력합니다. 그렇다면 최적 솔루션은 무엇입니까?
print(str(pulp.LpStatus[solution])+" ; max value = "+str(pulp.value(linearProblem.objective))+
" ; x1_opt = "+str(pulp.value(x1))+
" ; x2_opt = "+str(pulp.value(x2)))
Optimal ; max value = -19.999999999995993 ; x1_opt = 1.0018653e-12 ; x2_opt = 10.0
이 접근법은 x1 = 0 및 x2 = 10이 최적의 솔루션임을 제안합니다. 최적의 목표 값은 목표 1의 경우 30이고 목표 2의 경우 -20입니다.
접근 방식 2 : 샘플링 된 가중치 및 정의 된 단계 크기로 반복을 사용하여 목표 결합
이 접근 방식을 적용 할 때 원래 문제를 다음과 같이 다시 설명합니다.

이제 문제는 α를 선택하는 방법입니다.
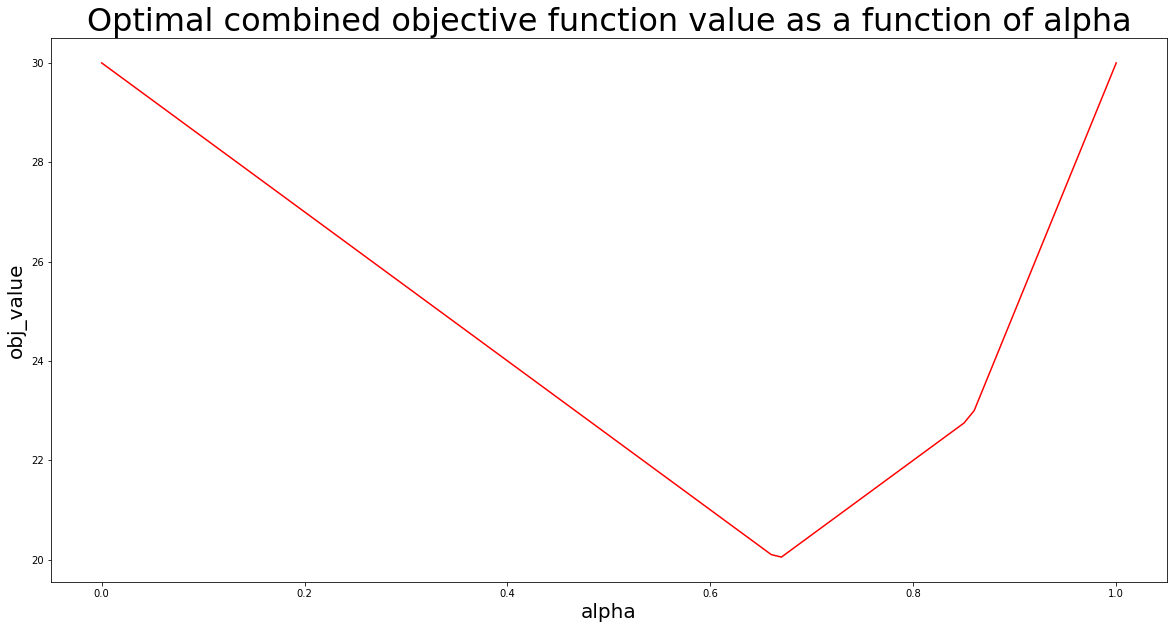
이와 같은 상황에서 일반적인 접근 방식은 효율적인 경계를 식별하는 것입니다. 경제학에서 이것은 예입니다. “파레토 최적 성”으로 알려져 있습니다. 이러한 접근 방식을 구축하기 위해 0.01 단계로 알파를 샘플링합니다. 각 알파 값에 대해 PuLP를 사용하여 문제를 다시 설명하고 해결합니다.
결과를 목록에 저장하고 matplotlib.pyplot을 사용하여 결과를 시각화합니다.
# import matplotlib.pyplot import matplotlib.pyplot as plt # DataFrame 형식으로 데이터를 저장할 수 있도록 pandas 및 numpy 가져 오기 import numpy as np import pandas as pd # 스텝 크기 정의 stepSize = 0.01 # 최적화 결과를 저장하기 위해 빈 DataFrame을 초기화합니다. solutionTable = pd.DataFrame(columns=["alpha","x1_opt","x2_opt","obj_value"]) # stepSize를 사용하여 0에서 1까지 알파 값을 반복하고 PuLP 솔루션을 solutionTable에 씁니다. for i in range(0,101,int(stepSize*100)): # 문제를 다시 선언 linearProblem = pulp.LpProblem("Multi-objective linear maximization",pulp.LpMaximize) # 샘플링 된 알파에 목적 함수 추가 linearProblem += (i/100)*(2*x1+3*x2)+(1-i/100)*(4*x1-2*x2) # 제약 추가 linearProblem += x1 + x2 <= 10 linearProblem += 2*x1 + x2 <= 15 # 문제를 풀다 solution = linearProblem.solve() # DataFrame에 솔루션 쓰기 solutionTable.loc[int(i/(stepSize*100))] = [i/100, pulp.value(x1), pulp.value(x2), pulp.value(linearProblem.objective)] # matplotlib.pyplot을 사용하여 최적화 결과 시각화 #-그림 크기 설정 plt.figure(figsize=(20,10)) #-라인 플롯 생성 plt.plot(solutionTable["alpha"],solutionTable["obj_value"],color="red") #-축 레이블 추가 plt.xlabel("alpha",size=20) plt.ylabel("obj_value",size=20) #-플롯 제목 추가 plt.title("Optimal combined objective function value as a function of alpha",size=32) #-플롯 표시 plt.show()

이 기사를 완료하기 위해 최적화 결과 DataFrame 테이블의 헤드를 인쇄합니다.
solutionTable.head()
| | alpha | x1_opt | x2_opt | obj_value |
|---|---|---|---|---|
| 0 | 0.00 | 7.5 | 0.0 | 30.00 |
| 1 | 0.01 | 7.5 | 0.0 | 29.85 |
| 2 | 0.02 | 7.5 | 0.0 | 29.70 |
| 3 | 0.03 | 7.5 | 0.0 | 29.55 |
| 4 | 0.04 | 7.5 | 0.0 | 29.40 |

최적화 및 시뮬레이션을 전문으로하는 산업 엔지니어 (R, Python, SQL, VBA)




Leave a Reply