En algunas de mis publicaciones utilicé lpSolve o FuzzyLP en R para resolver problemas de optimización lineal. También he usado PuLP y SciPy.optimize en Python para resolver este tipo de problemas. En todos esos casos el problema tenía una sola función objetiva.
En esta publicación, quiero proporcionar un ejemplo de codificación en Python, utilizando el módulo PuLP para resolver un problema de optimización lineal multiobjetivo.
Un problema de optimización lineal multiobjetivo es un problema de optimización lineal con más de una función objetivo. Esta área de programación lineal también se conoce como programación lineal multiobjetivo o programación lineal multiobjetivo.
A continuación, expuse un problema de optimización lineal multiobjetivo ejemplar con dos funciones objetivo:

Suponiendo que en el planteamiento del problema anterior las dos funciones objetivas representan dos metas diferentes, como p. Ej. nivel de servicio y margen de beneficio de alguna cartera de productos, pruebo dos enfoques alternativos para resolver este problema.
El primer enfoque será resolver uno de los objetivos, luego solucionar el problema en el resultado óptimo de ese primer problema agregando una restricción adicional a una segunda ejecución de optimización donde luego maximizaré la segunda función objetivo (sujeto a la restricción de manteniendo el valor objetivo óptimo para el primer subproblema).
El segundo enfoque consistirá en sumar los dos objetivos, es decir, fusionarlos en una función objetivo aplicando ponderaciones. Tomando muestras de las ponderaciones y resolviendo el problema combinado para cada ponderación muestreada, se puede revisar el resultado óptimo en dependencia de las ponderaciones.
Enfoque 1: maximizar para un objetivo, luego agregarlo como una restricción y resolver el otro objetivo
Usando PuLP maximizo el primer objetivo primero, luego agrego esa función objetivo como una restricción al problema original y maximizo el segundo objetivo sujeto a todas las restricciones, incluida esa restricción adicional.
En sintaxis matemática, el problema que resolvemos primero se puede plantear de la siguiente manera:

Aquí está la implementación de la declaración del problema anterior en Python, usando el módulo PuLP:
# primero, importa PuLP
import pulp
# luego, realice la declaración inicial del problema
linearProblem = pulp.LpProblem("Maximizing for first objective",pulp.LpMaximize)
# declarar variables de optimización, usando PuLP
x1 = pulp.LpVariable("x1",lowBound = 0)
x2 = pulp.LpVariable("x2",lowBound = 0)
# agregar (primera) función objetivo al enunciado del problema lineal
linearProblem += 2*x1 + 3*x2
# agregue las restricciones al problema
linearProblem += x1 + x2 <= 10
linearProblem += 2*x1 + x2 <= 15
# resolver con el solucionador predeterminado, maximizando el primer objetivo
solution = linearProblem.solve()
# información de salida si se encontró el óptimo, cuál es el valor objetivo máximo y cuál es el punto óptimo
print(str(pulp.LpStatus[solution])+" ; max value = "+str(pulp.value(linearProblem.objective))+
" ; x1_opt = "+str(pulp.value(x1))+
" ; x2_opt = "+str(pulp.value(x2)))
Optimal ; max value = 30.0 ; x1_opt = 0.0 ; x2_opt = 10.0
Ahora, vuelvo a plantear el problema original de modo que la segunda función objetivo se maximice sujeta a una restricción adicional. Esa restricción adicional requiere que el primer objetivo sea al menos 30. Usando la sintaxis matemática, el problema que ahora resuelvo se puede enunciar de la siguiente manera:

Aquí está la implementación de la declaración del problema anterior en Python, usando PuLP:
# remodelar el planteamiento del problema
linearProblem = pulp.LpProblem("Maximize second objective",pulp.LpMaximize)
linearProblem += 4*x1 - 2*x2
linearProblem += x1 + x2 <= 10
linearProblem += 2*x1 + x2 <= 15
linearProblem += 2*x1 + 3*x2 >= 30
# revisar la declaración del problema después de la remodelación
linearProblem
Maximize_second_objective: MAXIMIZE 4*x1 + -2*x2 + 0 SUBJECT TO _C1: x1 + x2 <= 10 _C2: 2 x1 + x2 <= 15 _C3: 2 x1 + 3 x2 >= 30 VARIABLES x1 Continuous x2 Continuous
Ahora, resuelvo este problema, usando el solucionador predeterminado en PuLP:
# aplicar solucionador predeterminado
solution = linearProblem.solve()
# generar una cadena que resuma si se encontró el óptimo y, de ser así, cuál es la solución óptima
print(str(pulp.LpStatus[solution])+" ; max value = "+str(pulp.value(linearProblem.objective))+
" ; x1_opt = "+str(pulp.value(x1))+
" ; x2_opt = "+str(pulp.value(x2)))
Optimal ; max value = -19.999999999995993 ; x1_opt = 1.0018653e-12 ; x2_opt = 10.0
Este enfoque sugiere que x1 = 0 y x2 = 10 es la solución óptima. Los valores óptimos del objetivo serían 30 para el objetivo uno y -20 para el objetivo dos.
Enfoque 2: combinar objetivos, utilizando muestras de ponderaciones e iteraciones con un tamaño de paso definido
Al aplicar este enfoque, reformularemos el problema original de la siguiente manera:

La pregunta ahora es cómo elegir α.
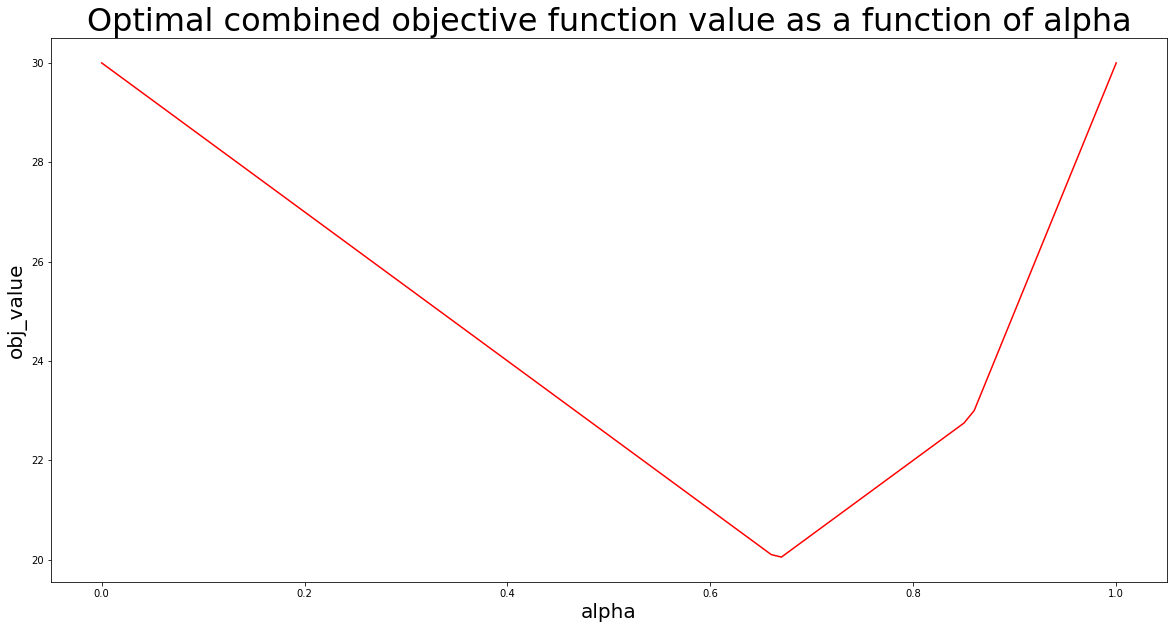
Un enfoque típico en una situación como esta es identificar una frontera eficiente. En economía esto es, por ejemplo, conocido como «Optimalidad de Pareto». Para construir un enfoque de este tipo, muestreé alfa en pasos de 0.01. Para cada valor de alfa, vuelvo a plantear el problema, usando PuLP, y lo resuelvo.
Guardo mis resultados en una lista y visualizo el resultado usando matplotlib.pyplot:
# importar matplotlib.pyplot import matplotlib.pyplot as plt # importar pandas y numpy para poder almacenar datos en formato DataFrame import numpy as np import pandas as pd # definir tamaño de paso stepSize = 0.01 # inicializar DataFrame vacío para almacenar resultados de optimización solutionTable = pd.DataFrame(columns=["alpha","x1_opt","x2_opt","obj_value"]) # iterar a través de los valores alfa de 0 a 1 con stepSize, y escribir soluciones PuLP en solutionTable for i in range(0,101,int(stepSize*100)): # declarar el problema de nuevo linearProblem = pulp.LpProblem("Multi-objective linear maximization",pulp.LpMaximize) # agregue la función objetivo en el alfa muestreado linearProblem += (i/100)*(2*x1+3*x2)+(1-i/100)*(4*x1-2*x2) # agrega las restricciones linearProblem += x1 + x2 <= 10 linearProblem += 2*x1 + x2 <= 15 # resolver el problema solution = linearProblem.solve() # escribir soluciones en DataFrame solutionTable.loc[int(i/(stepSize*100))] = [i/100, pulp.value(x1), pulp.value(x2), pulp.value(linearProblem.objective)] # visualizar el resultado de la optimización, usando matplotlib.pyplot # - establecer el tamaño de la figura plt.figure(figsize=(20,10)) # - crear diagrama de línea plt.plot(solutionTable["alpha"],solutionTable["obj_value"],color="red") # - agregar etiquetas de eje plt.xlabel("alpha",size=20) plt.ylabel("obj_value",size=20) # - agregar título de la trama plt.title("Optimal combined objective function value as a function of alpha",size=32) # - mostrar trama plt.show()

Para completar este artículo, imprimo el encabezado de la tabla DataFrame de resultados de optimización:
solutionTable.head()
| alpha | x1_opt | x2_opt | obj_value | |
|---|---|---|---|---|
| 0 | 0.00 | 7.5 | 0.0 | 30.00 |
| 1 | 0.01 | 7.5 | 0.0 | 29.85 |
| 2 | 0.02 | 7.5 | 0.0 | 29.70 |
| 3 | 0.03 | 7.5 | 0.0 | 29.55 |
| 4 | 0.04 | 7.5 | 0.0 | 29.40 |

Ingeniero industrial especializado en optimización y simulación (R, Python, SQL, VBA)




Leave a Reply